| Like Belgian Chocolate for the Universal Mind. Interpersonal and Media Gossip from an Evolutionary Perspective. (Charlotte De Backer) |
| home | list theses | contence | previous | next |
PART I
THEORETICAL FRAMEWORK
CHAPTER 5. Modeling the different kinds of gossip
“Results from the newly emerging field of evolutionary psychology suggest that (i) explicit, well-specified models of the human mind can significantly enhance the scope and specificity of economic theory, and (ii) explicit theories of the structure of the human mind can be made endogenous to economic models in a way that preserves and expands their elegance, parsimony, and explanatory power.” (Cosmides & Tooby, 1994a: 327).
Evolutionary biology not only has a tight connection with psychology, resulting in the field of evolutionary psychology, but can also be connected with economics. As Cosmides and Tooby (1994a) explained, natural selection is the blind process that slowly builds decision-making machinery in our minds, and these cognitive devices also generate economic behavior.
In the previous chapter, I focused on gossip as a noun, outlining how gossip as information can be classified in two well separated categories that each could solve adaptive problems occurring in the EEA. In this next step, I want to translate some of the different kinds of gossip in behavioral strategies, explaining what is going on when people exchange the kind of information that can be classified as gossip. For both Strategy Learning Gossip (SLG) and Reputation Gossip (RG) I will outline when it is advantageous to spread this kind of information around and when to pay attention to it. The stakes for SLG and RG are different. Costs and benefits for exchanging SLG are related to strategy knowledge, whereas the costs and benefits of RG concern both knowledge about and manipulation of reputations. The different costs and benefits involved, as well as other reasons I will discuss later, force me to outline different models for both.
This chapter is an exploratory part of my theoretical approach to gossip. I put forward some ideas about gossip that are new. Future research should investigate whether the models presented here are falsifiable. The primary scope of this chapter is to outline a manual to test whether the different kinds of gossip I distinguished in the previous chapter can be considered as adaptive or not. The focus of the previous chapter was to determine which functions could be attributed to gossip; this chapter tries to uncover the cognitive processes that underlie the different gossip adaptations.
2 Modeling human social behavior
2.1 Optimization models for human behavior
An evolutionary optimization approach is useful to construct a model about an adaptation. Parker & Smith (1990) set out some guidelines to construct optimization models. First of all, clear questions should be asked and these questions should be assumed to have an adaptive answer. Next, assumptions must be made about what should be maximized in terms of Darwinian fitness. Using optimization criterions, as indirect measures of fitness, assumptions must be made about the outcome of different strategies. This involves the construction of mathematical models to measure differences in outcomes. In a last step, the optimality approach should be tested, using observational data. Smith and Winterhalder (1992) give similar instructions, outlining as well that an optimization analysis is useful to compare different strategies an actor can choose between. For each alternative, costs and benefits have to be considered. An optimization analysis starts from an outline of which variables need to be maximized. Lastly, it is also important to recognize possible constraints (variables outside the actor’s control) that could determine the payoffs. There are however also some difficulties with these optimization models. For example, in real life an individual might not have access to all information needed to calculate the outcome (Parker & Smith, 1990).
2.2 Bounded rationality theory
2.2.1 The power of simple heuristics
Another critique on the optimization theory came from Herbert Simon (cited in Gigerenzer & Todd, 1999), who argued that humans are limited in their cognitive capacities, and optimization models are too complex to be considered as representations of human decision making. His ideas are used in the theory on Bounded Rationality, which I will use in this chapter to model how humans make decisions about “When to spread a certain gossip?”, “To whom should we tell the gossip?”, and “what do we have to pay attention to when confronted with gossip?”
The theory of Bounded Rationality focuses on fast and frugal heuristics that humans use to make decisions. “Fast and frugal heuristics employ a minimum of time, knowledge, and computation to make adaptive choices in real environments.” (Gigerenzer & Todd, 1999: 14). This theory builds on three (interconnected) domains of rationality: bounded rationality, ecological rationality and social rationality. The first domain of bounded rationality stresses the important fact that humans have limited time and capacity to make decisions. Ecological rationality refers to the fact that decision-making mechanisms (adaptations) exploit the structure of information in the environment, resulting in adaptive outcomes. Social rationality is a special form of ecological rationality and simply says that other agents are an important aspect of an agent’s environment. As Gigerenzer and Todd (1999) say, predators must make inferences about their prey, men and women must make decisions about others in the context of mating, etc. In the context of gossip, social rationality is obviously very relevant. Every decision that a sender or receiver of gossip has to make will always involve other agents.
A classical example of a fast and frugal heuristic is the recognition heuristic. Goldstein and Gigerenzer (1999) put forward and tested a simple rule that can solve problems in which an individual has to make inferences about which of two objects has a higher value. “The recognition heuristic for such tasks is simply stated: If one of two objects is recognized and the other is not, then infer that the recognized object has the higher value.” (Goldstein & Gigerenzer, 1999: 41). For instance when, asking non-German people which city is the biggest, Dortmund or Munich, many answer (correctly) ‘Munich’, because they recognize this city, and mostly non-Germans have not heard of Dortmund. Goldstein and Gigerenzer (1999) concluded from an experiment where people were asked which cities they recognized that the media influence our recognition heuristics. Bigger cities, with higher population rates should be recognized by more people, according to the recognition heurist.
They tested this among American students, and the correlation between people recognizing a German city and the city’s population is .60. Additionally Goldstein and Gigerenzer traced down all articles that had mentioned the name of these German cities in the issues of the past 12 year of the Chicago Tribune. The correlation between the city’s population and the times it was mentioned in the newspaper was .70 (ecological correlation). The stunning finding was that the correlation between the times a city was mentioned in the newspaper and the number of people who recognized the city was .79. “These results suggest that individual recognition is more in tune with the media than with the actual environment, which indicates that city name recognition may come largely from the media.” (Goldstein & Gigerenzer, 1999: 55). In chapter 7 (gossip and media) I will come back to this finding and relate it to media gossip.
2.2.2 Fast and frugal decision trees
Because mathematical optimization models are too complex to describe how humans make fast decisions, I will focus in this chapter on another method that better portrays human decision making. Katsikopoulos and Martignon (2003) have suggested that human decision making most often involves classification of different options. We use cues, or criterions (c), to guide our decision making. For each criterion estimations have to be made. E is called the criterion estimator. If E(c)= 1 this means that what is subjected to the criterion estimator is classified as passing the criterion positively. If E(c)= 0 this means that what is subjected to the criterion estimator is classified as passing negatively.
Such classification rules can be presented graphically in a classification tree. Such trees classify decision rules. Each node of a tree represents a question regarding certain features of the objects that need to be classified. Each branch of these nodes leads to an answer of the question. The nodes below other nodes are called “children”, and the higher level nodes “parents”. So-called “leaf” nodes are nodes that have no children (Martignon, Vitouch, Takezawa & Forster, 2003). The convention rule is that all “yes” answers drop off the left part of the question node, and all “no” answers drop off the right part of the question node (Katsikopoulos & Martignon, 2003). Branches that drop off the left are given the label “1”, while branches that drop off the right part of the node are given the label “0” (Martignon et al, 2003). The algorithm for classification trees is as following:
Algorithm TREE-CLASS:
(1) Begin at root node.
(2) Execute rule associated with current node to decide which arc to traverse.
(3) Proceed to child at end of chosen arc.
(4) If child is a leaf node, assign to object the class label associated with node and STOP.
(5) Otherwise, go to (2). (Martignon et al, 2003: 191).
Within these classification trees “Fast and Frugal Decision Trees” are trees where parent nodes have two children each and that allow classifications to be made at each level. At each level a leaf node is present (Katsikopoulos & Martignon, 2003, Martignon et al, 2003):
A fast and frugal binary decision tree is a decision tree with at least one exit leaf at every level. That is, for every checked cue, at least one of its outcomes can lead to a decision. In accordance with the convention applied above, if a leaf stems from a branch labeled 1, the decision will be positive. […]” (Martignon et al, 2003: 197)
Such fast and frugal decision trees perform not as good as rational computational models, such as logistic regression. Still, their performance is not dramatically lower, and these trees are far more easy to use (Martignon et al, 2003). Full mathematical models might still have stronger accuracy, but can not represent how human make decisions in real life, and: “[i]n many decisional domains, we may be better off trusting the robust power of simple decision strategies rather than striving for full knowledge of brittle details.” (Martignon et al, 2003: 210).
In this chapter I will use mathematical models to explain why we share Strategy Learning Gossip and Reputation Gossip. Sharing (gossip) information requires some more explanation than acquiring information. For both sharing and acquiring Strategy Learning and Reputation Gossip I will put forward classification trees. I will try to make these trees fast and frugal, with binary options and a leaf node at each level. Before doing this, however, I present some theoretical background on the sharing and acquiring of information.
3 Acquiring and sharing information
Both Strategy Learning Gossip (SLG) and Reputation Gossip (RG) involve the exchange of information. Certain costs and benefits are common for both kinds of gossip. I will outline these first, and then focus more specific on SLG and RG separately when translating these costs and benefits in optimization models and fast and frugal decision trees. In general, I will pay more attention to the sharing of both SLG and RG, because in evolutionary terms acquiring fitness-relevant information has clear benefits, but sharing this with others needs some more explanation.
3.1 Acquiring information
According to Michele Scalise Sugiyama (1996), it is the receiver of a story who benefits most from storytelling, because he or she gains social information about his or her environment. In her view, gossip is most beneficial for recipients. Or at least, this should be true for Strategy Learning Gossip (SLG), which in function is closely related to the function Scalise Sugiyama (1996, 2001) attributes to storytelling. Indeed, acquiring information, both behavior focused (SLG) or person focused (Reputation Gossip) requires very little investment of the listener. He or she just has to devote some of his or her time to the one who wants to share the gossip with them, knowing that they can gain a lot form this transaction.
Yet, besides this little cost of investing time to listen, the higher price people pay for new knowledge is the struggle with the question how reliable their news source is. Reliability is a major issue when we talk about gossip. Gossip has been called ‘cheap’, because it is so easy to lie (Barkow, 1989; Power, 1998). Even more troubling is the fact that true/not-true is no matter of black and white, but covers different shades of gray. There are might-be-true, what-others-believe-is-true, once-was-true, might-become-true, what-they-want-me-to-believe-true etc. (Tooby & Cosmides, 2001).
The first time you are presented a gossip story the news value will be high, but the credibility value might be low (depending on the credibility status of the source as well). Hearing the same piece of gossip multiple times might still be beneficial to add up credibility value (see chapter 1 as well). Hess and Hagen (2002) already noticed from their research on gossip among sorority girls that when the girls heard the same gossip story twice, it is when a reiteration effect is present, they were more likely to believe the gossip story. When independent sources spread the same gossip information, the believability of the gossip story still increases. Independency of the sources is important. When girls hear the same gossip story from several others who are close to each other, they were less likely to believe the gossip story, Hess and Hagen noticed. In sum, gossip, reported by multiple female sources, is more likely to be believed when these sources are independent instead of dependent of each other. Wilson et al (2000) found similar results for both male and female students, using paper-and-pencil test to investigate the importance of the reliability of the source(s) of a gossip story.
The importance of the reliability of the resource of gossip is not only important in the context of interpersonal gossip, as above described studies have shown, but also with media gossip. Kaufman, Stasson and Hart (1999) analysed the importance of source credibility of media gossip messages by comparing a rather untrustworthy newspaper (National Enquirer) with a more trustful one (Washington Post). Controlling for need-for-cognition they used a group of respondents who were low in need-for-cognition, meaning that those people rely on simple heuristics to process information (such as a reliability cue) and a group of respondents who were high in need-for-cognition. Those last always process information very thoroughly, and do not rely on peripheral cues. Those who score high on need-for-cognition are always cautious about information, but those who are low on need-for-cognition, are only sensible about the information when the source is rather unreliable. “When articles are attributed to low-credibility sources, the untrustworthy source may motivate greater scrutiny among individuals low in need for cognition.” (Kaufman et al, 1999: 1994.).
3.2 Sharing information
3.2.1 Low cost of sharing non-rival goods
In evolutionary terms, it is highly beneficial to get information, but less beneficial to share valuable knowledge with others. Sharing needs an explanation in evolutionary terms, as I explained in the previous chapter. The important difference between sharing goods, and sharing knowledge (which is the case with gossiping) is, as Romer (1994) outlined, that gossip can be considered as a non-rival good, for which the cost of sharing is relatively cheap. Sharing knowledge with others does not imply you lose it yourself, as is the case when you share goods. The costs of sharing non-rival goods, such as information, are low, while the benefits can be large, and basically concern reciprocal actions.
3.2.2 Multiple benefits of sharing gossip
3.2.2.1 Gossiping and kin selection
Following Hamilton’s (1964) thoughts on kin selection theory, I argue that gossiping can contribute to an individual’s inclusive fitness. Sharing fitness-relevant information (SLG) with kin, or increasing the status of kin related members through reputation gossip (RG), both rebound to individual benefits. You can secure or increase the fitness of relatives through SLG, and increase the reputation of relatives through RG.
I even expand this benefit of gossiping to coalitions. Individuals do not solely benefit from manipulating knowledge (SLG) and reputations (RG) of kin related members of their band, but also by doing this for coalition members. Increasing the knowledge and reputations of your own band (coalition) and securing that information is withheld from other bands (non-coalitions) or sharing false, deceitful knowledge with non-coalition members (false SLG), and decreasing the reputations of non-coalition members (negative RG) all rebound to relative benefits for an individual. If the level of truthful knowledge or the reputations of non-coalition members go down, the relative knowledge and reputation of the individual (and his coalition members) goes up.
3.2.2.2 Gossiping and reciprocal altruism
Though focusing on rumors, rather than on gossip, Rosnow and Fine’s (1976) ideas about rumors as a social exchange paradigm are applicable to gossip as well; “[…] like rumormongering, gossiping has definite functions that might best be understood within the framework of social exchange.” (Rosnow & Fine, 1976: p. 93). Indeed, Trivers’ (1971) simple principle of you-scratch-my-back-and-I’ll-scratch-yours can in this context be translated as you-tell-me-something-and-I’ll-tell-you-something.
But the returns go beyond informational benefits. Reciprocity in the context of gossiping has a broader perspective, say Rosnow and Fine (1976). We not only gossip to get information in return, but also to get money, power, status, etc.:
“From the broader perspective of social exchange, one can readily visualize rumormonging as a transaction in which someone passes a rumor for something in return – another rumor, clarifying information, status, power, control, money, or some other resource. When information is scarce, the rumormonger can exact a high price for his tales.” (Rosnow & Fine, 1976)
Sharing gossip can also assure the sender that the content is true: “What, in economics of gossip, is offered, what is received? Point of view, information; also reassurance. Participants assure one another of what they share: one of gossip’s important purposes.” (Spacks, 1985: 22).
3.2.2.3 Gossiping and the show-off hypothesis
Being rewarded with an increase of status, fits in the show-off hypothesis of explaining human sharing. The reason why we attribute status to people who share gossip with us, is according to Miller (2000), because having exclusive social knowledge signals high social status and intelligence. Therefore Miller claims that spreading gossip must have been favored by sexual selection. Pinker (1994) as well mentions that the leaders of current hunter-gatherer societies are often those who know most about what is going on in their band; they have information, power, and have high social intelligence skills.
This benefit of gossip sharing, however, involves a potential cost. One can loose exclusive social knowledge, if others run of with the gossip story (see below as well). To reduce this cost as much as possible, the sender must assure that he is recognized as the source of information. The easiest and most reliable way to achieve this is to spread the word around himself or herself to as many people as possible. “Hey, have you heard… but do not tell this to others” is a classical utterance when gossip is shared and can be associated with the thought “Because I will tell the others.”
Another important remark here is that prestige will only be given to those who spread true gossip. Spreading lies about other people will not increase your status, and can even harm your reputation. People are aware of this, because they are less likely to spread information of which they doubt the reliability. Jaeger, Anthony and Rosnow (1980) found that the reliability of the source and the content of information spread around influences the dissemination. The subject of their research were ‘rumours’, which they defined as “A rumor is a proposition for belief in general circulation without certainty as to its truth.” (Jaeger, et al, 1980: p. 473). Nevertheless, the ‘rumor’ they used concerned the smoking of marijuana by some students. So it is information about (a) person(s), which makes it very close to my definition of gossip. They called their information rumors, because they manipulated the believability of the story, by adding a confirmation (believable) or counter-statement (unbelievable) from an extra source. Their “[…] results suggest that a rumor perceived to be false is less likely to be transmitted than one perceived to be true.” (Jaeger et al, 1980: p.476).
3.2.2.4 Gossiping and tolerated scrounging
A fourth model that explains human sharing is tolerated scrounging (Gurven, in press). In this case people share their goods because the costs of defending them are too big. For instance, it is better to share large game that cannot be consumed alone. The cost of defending it would be big, and hungry others can benefit a lot if you give some away. In the context of gossip transactions this is an interesting way to explain why people tolerate that others run away with their knowledge. This is, if you share exclusive social knowledge with others, this can result in (1) an increase of social status and (2) the potential of getting return-information. It is in the interest of every individual to secure that he or she shares his or her knowledge with as many others as possible, so that the returned benefits are maximized. In reality however, recipients of gossip ‘run away’ with this knowledge, because they can profit from an increase in social knowledge and potential returned-information as well. People seem to tolerate this, and I guess tolerated scrounging can explain why. The cost of securing others that they will not spread around your knowledge are too high, because this would mean that an individual should spy on all his recipients, to secure that they do not run away with their knowledge. Additional, if others run off with the knowledge, this can increase the credibility of the gossip message, because hearing the same gossip story from multiple sources increases credibility (see above).
4 Exchanging Strategy Learning Gossip
The different kinds of SLG I differentiated between in the previous chapter (Survival, Mating, and Social SLG) all concern the sharing and acquiring of fitness-relevant information. Costs and benefits for all three kinds of gossip involve the manipulation of fitness-relevant knowledge of the receivers. Central to SLG is that the costs and benefits relate to information about fitness relevant strategies (knowledge) and this both for the sender and the receiver. The gossipees of SLG are mere carriers of information and are not subject to benefits of costs of the gossip transaction about their experiences.
In what follows, I put forward a general model that describes when it is optimal to share SLG. I pay more attention to explaining why we share SLG than to why we acquire SLG. This for the simple reason, as already explained, that sharing needs more explication from an evolutionary point of view. I first outline an optimisation model to clarify the costs and benefits of the sharing of SLG-exchange and then turn to classification trees that present a more realistic view on how humans make decisions about their daily gossip exchange. With these classification trees I also pay attention to the receiver’s side. Next to presenting classification trees that show how human decision-making occurs when SLG is shared, I also set up classification trees that clarify what receivers of SLG need to decide when hearing SLG, and how they best act on this acquired information.
4.1 Sharing Strategy Learning Gossip
Because the sender of SLG can manipulate the knowledge about fitness-relevant strategies of others, sharing SLG returns benefits. When sharing SLG the sender manipulates the knowledge of receivers. It is important to keep this in mind, and I remind again that the gossipees of SLG are no subjects of manipulative costs and benefits; gossipees are not at stake in the costs and benefits of sharing SLG. As I will discuss later, this is different for Reputation Gossip, where gossipees are at stake. I will first outline the costs and benefits of sharing SLG, and then put forward a fast and frugal decision tree to explain how humans decide when to share their fitness-relevant knowledge with others or not.
4.1.1 Costs and benefits of sharing Strategy Learning Gossip
4.1.1.1 Benefits of sharing SLG
The benefits of sharing SLG with others are twofold. First of all, the sender of SLG gets merit from people who believe him or her. Reason for this is because he or she shows off to have exclusive social knowledge. This happens regardless of the fact that the gossip story is true or not, but depends on the fact whether the gossip message is believed to be true or not. If everybody knows already what a sender of SLG is sharing, he or she does not signal exclusive social knowledge of course, and will not be merited for this. But, in a situation where some know the SLG message and a sender shares this SLG message with a receiver who knew about this already, this sender can still gain some merit. He or she does not show off complete exclusive knowledge, but rather exclusive knowledge (only some know about this).
Secondly, the one who shares SLG can manipulate the knowledge of others. Beneficial for the sender is to spread true-SLG to coalition members and withhold this from non-coalition members. Similar, he or she should withhold untrue-SLG from coalition members and make sure this reaches non-coalition members. Extra benefits are expected for the sender of true-SLG when he or she is kin related to the receiver of his or her SLG. He or she then increases his or her own inclusive fitness. Sharing SLG, the sender can manipulate (increase or decrease) the waste of time, energy and risks of receivers, by giving them strategy learning information that third parties (gossipees) have acquired by investing their time, energy and risks. The most beneficial for an individual in manipulating SLG is to secure that his or her relatives, friends, and other allies will increase future opportunities for fitness-promoting strategies and decrease future risks of fitness-endangering strategies. Likewise, an individual benefits from securing that non-allies will miss out on future opportunities for fitness-promoting strategies and will increase fitness-endangering strategies. If non-allies’ fitness goes down, the individual and his or her allies’ relative fitness goes up.
4.1.1.2 Costs of sharing SLG
The costs a sender of SLG has to take into account are threefold. A first cost is that when recipients do not believe the SLG, the sender can loose social status for having exclusive knowledge. If recipients do not believe the sender, and consider him or her as a liar, this decreases his or her social status for knowledge. Secondly he or she risks spreading around false knowledge. Doing this, he or she can decrease the fitness of others, if he or she causes them to use a strategy that will harm them in stead of being beneficial. This implies a cost if this happens to coalition members, and especially if this happens to kin related members (because of inclusive fitness). A third cost occurs when others run-off with the knowledge.
4.1.2 Mathematical model for sharing Strategy Learning Gossip
If I line up these costs and benefits in a mathematical optimization model, this looks as follows:
SK.(bCM + bNCM) + t.(bCM +k1 + dNCM - k5 + eNCM – k6) + u.(bNCM –k4 + dCM +k2 + eCM +k3)
>
SK.(dCM + dNCM) + u.(bCM +k1 + dNCM –k5 + eNCM –k6) + t.(bNCM –k4 + dCM +k2 + eCM +k3)
Where:
CM = coalition member receivers
NCM= non-coalition member receivers
b = number of people who believe you
d = number of people who disbelieve you
e = error (people who do not hear the gossip)
b + d + e = n = total number of coalition or non-coalition members (band)
nCM = bCM + dCM + eCM
nNCM = bNCM + dNCM + eNCM
SK= Social Knowledge
Senders of SLG show of exclusive Social Knowledge.
SK can vary from 0 to 1.
SK = 0 if everyone already knows the gossip information
SK = 1 if the sender has exclusive gossip information
Note that SK at the left side of the ‘>’ (benefits) means bonus points, or benefits to the sender: he or she gets merit for having Social Knowledge in the eyes of the receivers who believe him. The more receivers believe him, the more merit the sender gets (SK gets multiplied with (bCM + bNCM)
SK at the right side of the ‘>’ (costs) means punishment for being seen as a liar, or costs to the sender: he or she gets punishments from all receivers who do not believe the gossip message (SK here gets multiplied with (dCM + dNCM)
t = true SLG knowledge
u = untrue SLG knowledge
k1; k2; k3; k4; k5; k6 = corrections for kin relatedness with coalition and non-coalition members
where:
r= Wright’s coefficient of relatedness, with r(.5) for parents and siblings, r(.25) for aunts, uncles, and grandparents , r(.125) for cousins and stepsiblings, …and r(0) for non relatives
and:
k1 = n1.bCM.r(.5) + n2.bCM.r(.25) + n3.bCM.r(.125) + …
Where:
n1.bCM = number of coalition members who believe sender and with whom r = .5
n2.bCM = number of coalition members who believe sender and with whom r = .25
n3.bCM = number of coalition members who believe sender and with whom r = .125
k2 = n1.dCM.r(.5) + n2.dCM.r(.25) + n3.dCM.r(.125) + …
Where:
n1.dCM = number of coalition members who disbelieve sender and with whom r = .5
n2.dCM = number of coalition members who disbelieve sender and with whom r = .25
n3.dCM = number of coalition members who disbelieve sender and with whom r = .125
k3 = n1.eCM.r(.5) + n2.eCM.r(.25) + n3.eCM.r(.125) + …
Where:
n1.eCM = number of coalition members who do not receive the SLG and with whom r = .5
n2.eCM = number of coalition members who do not receive the SLG and with whom r = .25
n3.eCM = number of coalition members who do not receive the SLG and with whom r = .125
k4 = n1.bNCM.r(.5) + n2.bNCM.r(.25) + n3.bNCM.r(.125) + …
Where:
n1.bNCM = number of non-coalition members who believe sender and with whom r = .5
n2.bNCM = number of non-coalition members who believe sender and with whom r = .25
n3.bNCM = number of non-coalition members who believe sender and with whom r = .125
k5 = n1.dNCM.r(.5) + n2.dNCM.r(.25) + n3.dNCM.r(.125) + …
Where:
n1.dNCM = number of non-coalition members who disbelieve sender and with whom r = .5
n2.dNCM = number of non-coalition members who disbelieve sender and with whom r = .25
n3.dNCM = number of non-coalition members who disbelieve sender and with whom r = .125
k6 = n1.eNCM.r(.5) + n2.eNCM.r(.25) + n3.eNCM.r(.125) + …
Where:
n1.eNCM = number of non-coalition members who do not receive the SLG and with whom r = .5
n2.eNCM = number of non-coalition members who do not receive the SLG and with whom r = .25
n3.eNCM = number of non-coalition members who do not receive the SLG and with whom r = .125
This formula outlines most of the costs and benefits I summed up earlier. First of all the sender’s knowledge status is at stake. If recipients believe the sender of SLG, they will attribute knowledge status to the sender. The SK.(bCM + bNCM) in the formula simply stands for the total amount of people (coalition and non-coalition members) who believe the SLG sender. Likewise the SK.(dCM + dNCM) stands for the total amount of people who received the gossip and did not believe the sender.
As I explained above, SK can vary from value ‘0’ to value ‘1’. SK gets value 0 if everyone already knows the information, then the sender cannot show off exclusive social knowledge. SK gets the maximum value of ‘1’ if he or she is (almost) the only one who knows the gossip information. That is why senders must secure to spread the news to as many people as possible as the first sender; the more people know the information, the higher the chances that potential receivers will have already heard the information (the cost of runaway knowledge). SK can have a value in between ‘0’ and ‘1’ if the receiver already knew the information, but knows that only a few people know about the gossip information. The sender does not get maximum merit, but still gets some merit because he or she signals he or she is one of the few people who know about this.
If for instance a sender has exclusive social knowledge (SK= 1), he or she only gets merit from those who believe him or her. A sender gains social knowledge status from every receiver who believes him or her and looses social knowledge status from every disbeliever. If for instance a sender tells a SLG to 20 people, of which 15 believe the SLG and 5 do not, the sender gets an increase of 15 points from the 15 believers, and loses 5 points from those who disbelief him or her. His or her net benefit is 10 points of social knowledge credit.
Next, the knowledge of the receivers is at stake. If the SLG is believed to be true (t=1 and u=0), the sender must secure that this true-SLG, which has clear fitness benefits, reaches coalition members who believe the sender, and does not reach non-coalition members or if it reaches non-coalition members they best do not believe this true-SLG. This is formula with t.(bCM + dNCM + eNCM). For true-SLG the number of coalition members who believe the SLG (bCM) -and therefore benefit from fitness relevant true information- should be maximized. If the SLG is true, then the sender benefits most by not telling his or her non-coalition members (maximize eNCM) or securing that the non-coalition members disbelieve the information (maximize dNCM).
If the SLG is believed to be untrue by the sender (lie), then u=1 and t=0. In this case u.(bNCM + dCM + eCM) states that the number of non-coalition members believing the untrue SLG should be maximized (bNCM). And, if the SLG is untrue the sender benefits most if his or her coalition members do not hear the SLG (eCM) or disbelieve the false information (dCM).
Further, the formula also calculates corrections for kin relatedness. If the information is true (t=1) and a coalition member believes the SLG (bCM) then extra benefits comes from kin-relatedness: (t.k1). If a coalition member disbelieves the SLG (dCM) or does not hear the SLG (eCM) and the SLG is true, then a cost comes from the kin-relatedness (t.k2) or (t.k3). In this same situation where t=1 some benefits gets lost for non-coalition members who disbelieve (dNCM) or not hear the SLG (eNCM): (-t.k5) and (-t.k6). Still in this situation where t=1, some costs are reduced because of kin-relatedness: (-t.k4) for non-coalition members who do believe the SLG.
If the information is untrue (u=1) kin-relatedness increases some benefits and decreases a benefit. The fact that coalition members do not hear (eCM) or disbelieve (dCM) false SLG are benefits, to which kin-relatedness adds extra benefits: (u.k2) and (u.k3). In the situation that the SLG is untrue (u= 1) kin-relatedness increases a cost and reduces two costs. The fact that coalition members believe false SLG is a cost, and this costs is even higher for kin-related coalition members (u.k1). The fact that non-coalition members do not hear (eNCM) or disbelieve (dNCM) untrue SLG are costs as well, but if these non-coalition members are kin-related to the sender, the costs get a little reduced: (-u.k5) and (-u.k6).
4.1.3 Visual translation of domain of the model
What I described above can be visualized as follows:

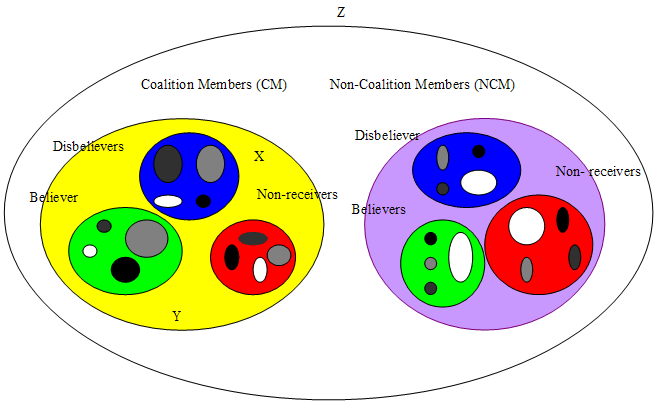
An individual X who sends a SLG about Y to a population Z, has a number of coalition members (yellow) and a number of non-coalition members (purple). Among X’s coalition members, some will hear the SLG from X (green and blue), and some will not (red). Among those X reaches, some will believe him (green) and some will not (blue). And for all these three groups (believers, disbelievers, non-receivers) some individuals will be kin related to X, and this with a varying degree (here black is r=.5; dark grey r=.25; light grey r=.125), and others will not be related to X (white r=0). Similar to the population of coalition members, the non-coalition members has believers, disbelievers, and non-receivers, with for each group kin-related and non kin-related individuals. In the EEA non-coalition members will have been mostly not kin-related. This will only be the case after relocation of individuals, which was mostly the case for women (at marriage).
4.1.4 Fictive examples of the mathematical model for sharing Strategy Learning Gossip
Let me illustrate and clarify this cost/benefit analysis with some fictive examples. I will present an optimal strategy example of sharing truthful SLG and an optimal strategy example of sharing untrue SLG (where the sender spreads a lie). I illustrate the formula in the context of simple coalition structures, as was the case in the EEA. I do admit that nowadays our living structures are more complex, and it is difficult to define who our coalition members are and who are not (see next chapter).
4.1.4.1 Example 1: sharing exclusive (SK= 1) eye witness (t= 1) SLG
Imagine for instance that X has 100 coalition members and 200 non-coalition members he can gossip with. This is 100 people he lives with, and 200 he meets on visits, or at larger meetings, gatherings. He witnesses how a man is killed by an unknown snake. Seeing this he has knowledge of 100% true-SLG (t= 1 > u= 0). He is the only one who witnessed this, so has exclusive social knowledge, no one else has (SK= 1). He starts to spread the news around, to 110 people in total, of which 60 are coalition members (CM), and 50 are non-coalition members (NCM). He does not tell his other 40CM (eCM= 40), and 150NCM (eNCM= 150) with whom he has contact. Of the 60CM he tells the information, 50 believe him (bCM= 50), and 10 do not (dCM= 10). Of the NCM, 30 believe him (bNCM= 30) and 20 do not (dNCM= 20). His relatives are scattered over all groups. For an overview and calculations of k1 to k6 see table V.1.
Table V.1. Population overview of fictive examples and calculations of k’s.
|
|
Relatives |
Non-relatives |
||
|
|
r= .5 |
r= .25 |
r= .125 |
r = 0 |
|
Coalition members (CM = 100) |
|
|
|
|
|
believers (bCM = 50) |
5 |
10 |
20 |
15 |
|
k1 = 7.5 |
5/2 = 2.5 |
10/4 = 2.5 |
20/8 = 2.5 |
0 |
|
disbelievers (dCM = 10) |
0 |
1 |
3 |
6 |
|
k2 = .70 |
0 |
1/4 = .25 |
3/8 = .45 |
0 |
|
non-receivers (eCM = 40) |
0 |
0 |
20 |
20 |
|
k3 = 2.5 |
0 |
0 |
20/8 = 2.5 |
0 |
|
|
|
|
|
|
|
Non-coalition members (NCM = 200) |
|
|
|
|
|
believers (bNCM = 30) |
0 |
3 |
6 |
21 |
|
k4 = 1.5 |
0 |
3/4 = .75 |
6/8 = .75 |
0 |
|
disbelievers (dNCM = 20) |
0 |
0 |
2 |
18 |
|
k5 = .25 |
0 |
0 |
2/8 = .25 |
0 |
|
non-receivers (eNCM = 150) |
0 |
0 |
15 |
135 |
|
k6 = 1.875 |
0 |
0 |
15/8 = 1.875 |
0 |
If I fill in all values from this fictive example 1 into the formula to estimate the cost/benefits of spreading this gossip, this gives:
SK.(bCM + bNCM) + t.(bCM +k1 + dNCM - k5 + eNCM – k6) + u.(bNCM –k4 + dCM +k2 + eCM +k3)
>
SK.(dCM + dNCM) + u.(bCM +k1 + dNCM –k5 + eNCM –k6) + t.(bNCM –k4 + dCM +k2 + eCM +k3)
1.(50 + 30) + 1.(50 + 7.5 + 20 - .25 + 150 – 1.875) + 0.(30 – 1.5 + 10 + .70 + 40 + 2.5)
>/<?
1.(10 + 20) + 1.(30 – 1.5 + 10 + .70 + 40 + 2.5)
1.(50 + 30) + 1.(50 + 7.5 + 20 - .25 + 150 – 1.875)
>/<?
1.(10 + 20) + 1.(30 – 1.5 + 10 + .70 + 40 + 2.5)
80 + 225.375
>/<?
30 + 81.70
305.375 > 111.70
The sender of this example gained 50 points of social knowledge status (80 -30), the benefits of manipulating the knowledge of others is 225.375, which have to be reduced with 81.70 costs of manipulating the true knowledge of others.
4.1.4.2 Example 2: sharing untrue (u= 1) exclusive (SK=1) SLG
Now consider X spreads a lie to the same audience (see table V.1). He knows a man got killed by an unknown snake and shares with the receivers that he encountered an unknown snake. He is the only witness of this happening. He describes the snake accurately (he has exclusively witnessed the snake) and tells his friends and foes this animal is not dangerous. He therefore endangers the life of those who hear and believe this information. Here u=1. Let me now illustrate that this is a bad strategy of X:
SK.(bCM + bNCM) + t.(bCM +k1 + dNCM - k5 + eNCM – k6) + u.(bNCM –k4 + dCM +k2 + eCM +k3)
>
SK.(dCM + dNCM) + u.(bCM +k1 + dNCM –k5 + eNCM –k6) + t.(bNCM –k4 + dCM +k2 + eCM +k3)
1.(50 + 30) + 0.(50 + 7.5 + 20 - .25 + 150 – 1.875) + 1.(30 – 1.5 + 10 + .70 + 40 + 2.5)
>/<?
1.(10 + 20) + 1.(50 + 7.5 + 20 - .25 + 150 – 1.875) + 0.(30 – 1.5 + 10 + .70 + 40 + 2.5)
1.(50 + 30) + 1.(30 – 1.5 + 10 + .70 + 40 + 2.5)
>/<?
1.(10 + 20) + 1.(50 + 7.5 + 20 - .25 + 150 – 1.875)
80 + 81.70
>/<?
30 + 225.375
161.70 < 255.375
Costs outscore the benefits for X by sharing this lie with his friends and foes.
If he would have shared this information only with the foes, and not with the friends, then bCM=0 and dCM= 0, while eCM= 100, and the model would give the following results:
SK.(bCM + bNCM) + t.(bCM +k1 + dNCM - k5 + eNCM – k6) + u.(bNCM –k4 + dCM +k2 + eCM +k3)
>
SK.(dCM + dNCM) + u.(bCM +k1 + dNCM –k5 + eNCM –k6) + t.(bNCM –k4 + dCM +k2 + eCM +k3)
1.(0 + 30) + 0.(0+ 0 + 20 - .25 + 150 – 1.875) + 1.(30 – 1.5 + 0 + .0 + 0 + 0)
>/<?
1.(0 + 20) + 1.(0 + 0 + 20 - .25 + 150 – 1.875) + 0.(30 – 1.5 + 0 + 0 + 0 + 0)
1.(0 + 30) + 1.(30 – 1.5 + 0 + .0 + 0 + 0)
>/<?
1.(0 + 20) + 1.(0 + 0 + 20 - .25 + 150 – 1.875)
30 + 28.5
>/<?
20 + 168.10
58.5 < 188.10
Here costs still outscore the benefits, but not as much as in the previous example where X shares the false SLG with friends and foes. If X would increase the number of foes he shares this false knowledge with (eNCM decreases), and if among those receivers enough individuals believe X, he can be sure benefits of his actions will outscore costs.
4.1.5 Difference for fitness-promoting SLG and fitness-endangering SLG
In the model I just outlined, I did not make a difference for fitness-promoting or fitness-endangering information transmitted through SLG. There is a difference in cost- and benefit values, though, for these different kinds of gossip. Focusing on the difference in benefit value, consider the following examples. First example: “Have you heard that since Stan started going to the gym regularly he attracts so many women? He used to look chubby, but now he is in shape it seems like every woman who never even looked at him wants to date him now!” From this information male receivers can learn “If I got to the gym and get in shape, I can attract more women.”
The second example “Have you heard, Roseanne got killed by a shark?! She loved to go swimming with the seals, and they think a shark attacked her, thinking she was a seal!”. From this SLG (SLG2) the receiver can learn “If I swim with seals I risk to be eaten by a shark, so I will not swim with seals.”
As a third and last example: “Have you heard, Steve and Lisa went hiking, and Steve was bitten by a poisonous snake! He survived, because Lisa always carries a self-aid kit for snakebites when they go hiking. If she had not been able to give him the anti-poison he might have died, because they were too far away from a hospital!” This SLG (SLG3) transmits information on how to secure survival; it is fitness-promoting SLG. The strategy a receiver can learn is “If I go hiking, then I take a snake-bite kit along”, since this can save your life or that of others.
Now compare the benefits of SLG1, SLG2, and SLG3. If a receiver of SLG1 believes this gossip, and mimics the strategy (work out) this can increase his fitness (access to more mates for men). If the receiver of SLG2 believes the gossip and decides not to mimic the strategy (swimming with seals), this does not affect his or her fitness, he or she will not improve his or her health status. The receivers of SLG2 benefit from avoiding dangers, but this benefit value is lower than the benefit outcome of SLG1, where a clear increase of fitness follows from mimicking the strategy. For SLG3, receivers who believe the information and mimic the strategy (carry on first aid snakebite kit), save their lives when ending up in the same situation (bitten by poisonous snake). SLG1 and SLG3 have clear positive benefit outcomes when receivers mimic the behavior, whereas SLG2 does not lead to fitness-increase, but fitness-maintenance. In sum B1=B3>B2 (see table V.2).
Comparing the costs of the three examples, SLG1 does not imply immediate fitness loss to those who disbelieve or not receive the information. The cost of not hearing this SLG1 or not believing it is lost opportunities; missing valuable chances. The case is totally different for example SLG2. If people do not hear or disbelieve this information, and would go swimming with seals they risk to get killed by a shark. There are potential costs of not hearing and believing this warning SLG, that can result in (extreme) fitness-loss. The same is true for the third example; people not hearing the warning of SLG3 can risk their life when they go hiking, and do not carry on first-hand medication. For the costs C2=C3> C1. For an overview see table V.2.
When modeling SLG, different weights could be given to the costs and benefits of receiving and believing vs. not hearing or disbelieving. In table V.2 I gave a weight of 2 to costs benefits that had clear immediate fitness-relevant outcomes when the strategy would be mimicked, and gave the weight of 1 to costs and benefits that do not directly affect the fitness of receivers and non-receivers.
Table V.2. Different cost- and benefit values for fitness-promoting SLG and fitness-endangering SLG
|
|
Received SLG |
Not received SLG |
|
|
|
Believe (b) |
Disbelieve (d) |
No heard (e) |
|
Fitness promoting SLG (example SLG1) |
Hit opportunity B = 2 |
Miss opportunity C1 = 1 |
Miss opportunity C2 = 1 |
|
Fitness endangering SLG (example SLG2) |
Avoid danger B = 1 |
Risk danger C1 = 2 |
Risk danger C2 = 2 |
|
Combined SLG (example SLG3) |
Hit opportunity B = 2 |
Risk Danger C1 = 2 |
Risk Danger C2 = 2 |
It could even be further argued that high costs are more important than high benefits. “If I do this I can die” simply has more value than “If I do this my fitness increases significantly”, because of the death warn. Negative news has stronger impacts on individuals than positive news.
What is known as the ‘negativity bias’ explains why people are drawn more to negative news and events, and remember it better. It has been shown that negative information indeed has a greater impact than positive information, and is retained better (e.g. Ito, Larsen, Smith & Cacioppo, 1998). People more easily belief information about the immoral (negative) behavior of others than they belief information about moral (positive) behavior. Moreover, information about immoral behavior is regarded to have a greater news value (Lupfer, Weeks & Dupuis, 2000). Negative events seem to impact people stronger than neutral or positive events (Taylor, 1991). Rozin and Royzman (2001) have also argued that both innate predispositions and experience in both animals and humans give greater impact to negative entities such as events, objects and personal traits.
Learning how to escape danger is indeed more valuable than learning how to improve your well-being. Learning what can benefit you is of course beneficial, but missing such positive information does not decrease your fitness, you retain the fitness you have. Missing out on an opportunity to learn how you could have avoided an extremely dangerous situation can be extremely costly. If you missed this negative information you risk dying. This explains why people are more drawn to negative gossip than to positive gossip, and the negativity bias adds to this that we also remember this negative information better. In chapter 7 on Media Gossip, I will come back to this as well.
4.1.6 Decision trees for sharing Strategy Learning Gossip
Of course people do not make full cost/benefit analyses before they share SLG. Luckily, because otherwise not much fitness-relevant information would be shared. I will therefore outline which simple rules (fast and frugal decision rules) can better explain what is going on in the human mind when people decide when to share SLG, and when they decide not to. Making use of a tally tree structure, I lined up all criteria people use to determine whether to share or not to share SLG with others.
In the previous chapter I explained how we often mimic the overall behavior of higher status individuals, because it has been shown that mimicking higher status others can increase your own status (Henrich & Gil-White, 2001). Boyd and Richerson (1985) have suggested that selection most probably favored the strategy to copy the overall behavior of higher status others (General Copying Bias), because it is often hard to find out what exactly contributes to the high status of others.
I here put forward two trees for sharing SLG because the General Copying Bias can influence the decision process in two ways. Either individuals use a fully elaborated decision route, where the GCB only comes in at the end, or they use a less elaborated decision process where they rely on the GCB as one of the first decision criteria.
4.1.6.1 Fully elaborated decision process to decide when to share SLG
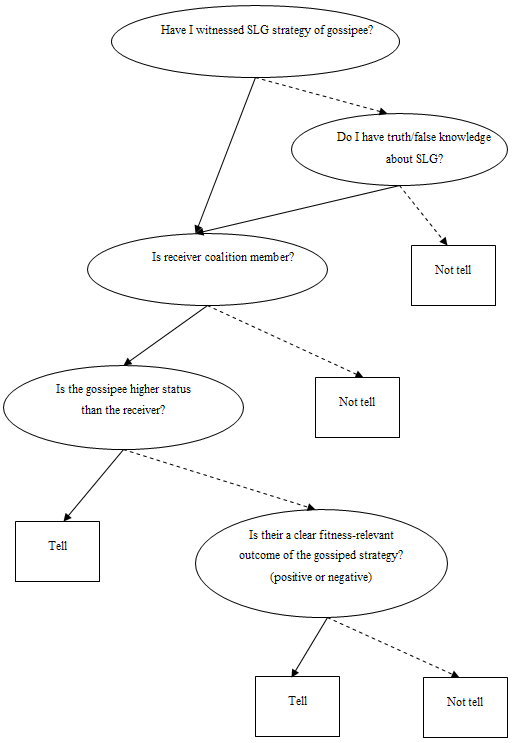
The truth value is important for SLG. Sharing false knowledge about fitness-relevant strategies can potentially endanger receivers. Making people believe something is dangerous when actually it is not, can lead them to miss opportunities, and even worse, making people believe something is safe when it is not, can be malign for their fitness. Therefore, senders of SLG should consider the trustworthiness of their information. Simple rules for this can be “Have I witnessed the strategy taking place?” If yes, then the sender can be sure the information is correct (t=1). If not, he or she can rely on the next criterion: “Do I know for sure that the SLG is true or false?” With this question the sender estimates if he or she has truth/false knowledge about the content of the information. Again, if yes, the sender can continue to the next criterion. If not, the sender best decides not to tell the gossip (or better rumor, since true/false knowledge is lacking), to rule out risks of getting punished on spreading false social knowledge, and rule out risking the fitness of coalition members. Deciding not to tell doubtful knowledge is a good and simple strategy.
If the information is likely to be absolutely true or absolutely false, the sender best asks next “Is the receiver a coalition member or not?”. If not, then not tell the SLG. If yes, two more criteria need to be considered. First, “Is the outcome of the behavior clearly fitness-relevant?”, if yes, then the sender should share the SLG, so that he or she can increase the fitness-relevant knowledge (experience relevant information) of the receiver (being a coalition member), which in the end rebounds to his or her own benefits. If there is no clear fitness-relevant outcome to the strategy, like e.g. “Ann ate a lot of apples when she was pregnant”, the sender can rely on the decision criterion “Is the gossipee higher status than the receiver?”. If no, then do not tell the gossip, if yes tell the gossip. This last criterion refers to the General Copying Bias (Boyd & Richerson, 1985) which states that we copy the overall behavior of prestigious people, in the believe that this can increase our own status (see previous chapter for more details). If the SLG would be “Madonna ate a lot of apples when she was pregnant.”, it would be more likely that this is shared with others, because of the prestige bias. I come back to this in the last chapter on media gossip as well.
All these decisions can be lined up in a sequential tree shown in figure V.2. In this figure, and all other decision trees full arrows are followed when the answer to the question is “yes” and dotted arrows are followed when the answer to the question is “no”.
4.1.6.2 Less elaborated decision process to decide when to share SLG
In a second decision process, senders of SLG can use the General Copying Bias as one of the first criteria to decide when to share and when not to share their SLG with others. In stead of first looking at the outcome of the gossiped about strategies, senders who use a less elaborated decision process first look at the status of the gossipee.
All decision criteria in this less elaborated decision process are similar to the decision criteria of the full elaborated decision process (see figures V.2 and V.3), but the order has changed. For both decision processes, senders first of all consider the reliability of the information. They will share if they know for sure the information is true, or if they know for sure the information is not true (intentional lie), and will not share if they have no truth/false knowledge about the information (the information is then classifiable as rumors).
Also the third criterion (is receiver ally or not) is the same for both decision processes. But the fourth and fifth criteria have switched places. Where elaborated decision makers first look at the outcome of the gossiped about strategy, the less elaborated decision makers use a faster and simpler decision criterion first. The fourth decision criterion for the less elaborated decision makers concerns the question “Is the gossipee higher status than the receiver or not?”.
Because in this decision process the sender does not look at the outcome of the gossiped about strategies first, all strategies are transmitted to receivers. This is, both strategies with a clear fitness-relevant outcome and unclear-outcome strategies are all shared with receivers who are lower status than the gossipee. Optimally, senders (and receivers) look first at the outcome of the gossiped about strategies and only after that rely on the status of the gossipee to decide if they want to share (or mimic) unclear-outcome strategies. Looking at the status first might be faster and easier to use as a decision criterion, but not the most optimal strategy.
For an overview of this less elaborated decision route I refer to figure V.3.
Figure V.2. Tally tree for sharing Strategy Learning Gossip, using a fully elaborated decision making process

Figure V.3. Tally tree for sharing Strategy Learning Gossip, using a less elaborated decision making process
4.2 Acquiring Strategy Learning Gossip
I now turn to models that predict the decision behavior of receivers of gossip. Acquiring fitness-relevant information is beneficial from an evolutionary perspective. However, acquiring Strategy Learning Gossip is not without potential costs. I do not put forward here a fully mathematical model, as I did to explain why we share Strategy Learning Gossip, but present two decision trees that outline the decision criteria receivers of SLG can use to come to an optimal use of receiving SLG.
4.2.1 Costs and benefits for acquiring Strategy Learning Gossip
The benefits of acquiring Strategy Learning Gossip are that an individual can learn how to improve his or her fitness or can learn about threats and dangers that can damage his or her fitness. SLG increases the experience knowledge of receivers, and can be stored in what Guth (2000) calls the Master Module, to fill one’s behavioral repertoire that can guide future decision making.
As for all kinds of gossip, and other forms of communication, the cost of acquiring information is that it might be false information. The reliability of the source is at stake, and this highly influences the receivers’ skepticism.
4.2.2 Decision trees for acquiring Strategy Learning Gossip
Receivers of SLG will pay attention to the reliability of the source. If the information is true, they can gain experience. If the information is false, they risk missing opportunities by getting false warnings and loosing time and energy in investment in false fitness-opportunities. The first and most important decision criterion for receivers of SLG will therefore be the reliability of the resource. If the SLG source is unreliable the receiver will not pay attention to, nor act on the content of the received SLG.
If the source of the SLG is reliable, the receiver must pay attention to some extra criteria that are quite similar to the criteria I outlined for sharing SLG. Again I put forward two different decision paths that explain how receivers act on acquiring SLG.
4.2.2.1 Fully elaborated decision process to decide when to act on acquired SLG
In a first model (see figure V.4), receivers use a fully elaborated decision process, carefully weighing costs and benefits of the gossiped about strategy. If the gossiped about strategy is costly to the gossipee and can be costly to the receiver when he or she mimics the strategy, the receiver optimally stores the SLG as ‘not to mimic strategy’. If he or she ends up in a similar situation in the future as the gossiped about situation, he or she will then be able to make a quick decision, not to act as the gossipee did. If the gossiped about strategy is clearly beneficial to the gossipee, and would be beneficial to the receiver as well if he or she mimics this strategy, the receiver optimally stores the SLG as ‘to mimic strategy’. In similar future situations this stored experience information can then help to quickly decide what to do. If the outcome of the gossiped about strategy is unclear, the receiver optimally ignores the SLG is the gossipee is not higher status than himself or herself. If the gossipee of the SLG is higher status than the receiver, he or she can best mimic the strategy. If the outcome is not clearly harmful or beneficial, not much damage can be done by mimicking the strategy, and moreover, since the gossipee is higher status mimicking his or her behavior might potentially increase the status of the receiver. This last is of course due to what the General Copying Bias predicts. In this ‘safe’ model, the General Copying Bias influences the decision pattern of the receiver at the end of an elaborated decision process. An overview of this elaborated decision process is given in figure V.4. Again full arrows are followed when the answer to the question is “yes”, and dotted arrows are followed when the answer to the question is “no”.
4.2.2.2 Less elaborated decision process to decide when to act on acquired SLG
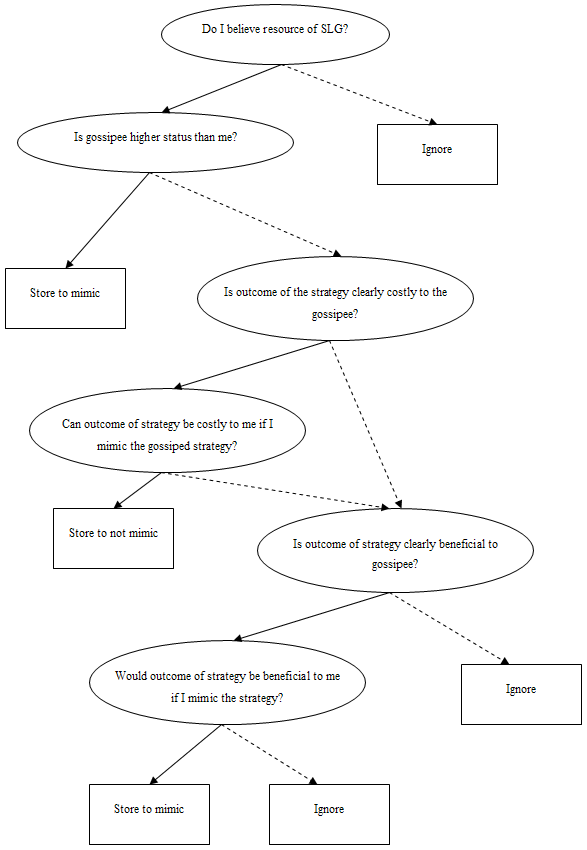
In a second, less elaborated decision tree (see figure V.5) that explains the decision a receiver of SLG optimally makes, the General Copying Bias operates at the beginning of the decision process. In stead of carefully weighing the costs and benefits of mimicking the gossiped about strategy, this decision process puts forward that the most optimal strategy is to look first at the status of the gossipee before paying attention to the transmitted behavior information. If the gossipee is higher status than the receiver, he or she optimally mimics the gossiped about strategy, since this can increase the status of the receiver. The General Copying Bias here distorts an elaborated decision path. Strategies with clear costly outcome are not filtered out of this process. If the gossipee of a costly strategy is higher status than the receiver of the SLG, the receiver will mimic this costly strategy in the aspiration to increase his or her status, while this mimicking behavior will impose costs to the receiver. This decision process is faster, less elaborated, than the first, since the criterion “Is the gossipee higher status than me?” will often lead to quicker decisions – to mimic. However, faster is not always most optimal, because of the risks that costly strategies might be mimicked. An overview of the less elaborated decision process to acquire and act on SLG can be found in figure V.5. Again full arrows are followed when the answer to the question is “yes” and dotted arrows are followed when the answer to the question is “no”.
Figure V.4. Fully elaborated decision process to acquire and act on Strategy Learning Gossip
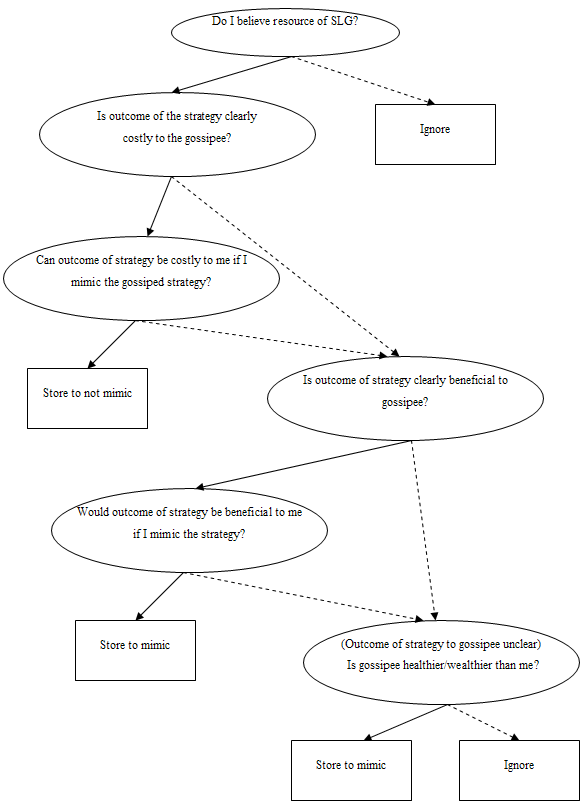
Figure V.5. Less elaborated decision process for acquiring and acting on Strategy Learning Gossip
5 Exchanging Reputation Gossip
In chapter four, I put forward different kinds of Reputation Gossip that each function to solve specific problems of human mating or group living. The important difference between Strategy Learning Gossip (SLG) and Reputation Gossip (RG) is that gossipees of the first function as mere carriers of strategy learning information, while the gossipees of the latter are the focus of the gossip content. RG is about traits and/or behaviors attached to a specific other individual. I have outlined above that the costs and benefits of sharing SLG concern the manipulation prestige of the sender and of knowledge of the receiver. For Reputation Gossip the costs and benefits of sharing are also related to the prestige of the sender and the knowledge of the receiver, but additionally also to the reputations of the gossipees.
Again I put forward a mathematical model to explain when it is optimal to share Reputation Gossip with others. For both sharing and acquiring RG, I present classification trees that better represent real life decision making. I do not present different models for the different kinds of RG that I distinguished between in chapter 4. This would lead me too far, as this chapter is just an exploratory exercise. I here take the first steps to translate my classification of the different kinds of gossip in behavioral models. I would like to suggest, however, that future research should first of all investigate whether my classification system covers all different kinds of gossip that nowadays exist and if changes to the classification system must be made. Only when this is done more specific behavioral models for the different kinds of RG should be constructed.
Still, I would like to comment that different kinds of RG have different value for receivers or senders of RG. Receivers of Reputation Gossip benefit most from forms of Detection RG, such as Kin Detection RG, Ally Detection RG, Mates Detection RG and Sexual Rival Detection RG. They also benefit from Mating Structure RG and Ally Structure RG, and from Calibration RG. Senders of Reputation Gossip benefit most from manipulative forms of RG, such as Mates Control RG, Sexual Rival Slander RG, Ally Maintenance RG. The models I put forward to explain the optimal strategy to share RG focus on these manipulative kinds of RG, while the classification trees for acquiring RG I will present focus in the detective kinds of RG.
5.1 Sharing Reputation Gossip
I start again with an outline of the optimal strategy to share Reputation Gossip with others. Again senders of RG give away their knowledge, and as before, this sharing of information requires more explanation than acquiring RG. I will first make a list of the specific costs and benefits associated with the sharing of RG. I will then put these costs and benefits in a mathematical model and a classification tree.
5.1.1 Costs and benefits of sharing Reputation Gossip
5.1.1.1 Benefits of sharing RG
The benefits of sharing RG are threefold. First of all, senders of RG can gain merit in the eyes of those who believe him or her. Similar to sharing SLG, sharing RG means that a sender shows off his or her exclusive social knowledge. Note again that this merit will not be present if everybody already knows what the sender of RG is telling. But, even if the information is not completely exclusive, senders of RG can gain merit. Situations where some people already know the RG message can still result in an increase of social knowledge status for the sender, if only a few know about the RG message. The information is then not completely exclusive, but quite exclusive (only some know about it).
Social knowledge status is not potentially present for all RG. Different from SLG, RG is not always about the behaviors of others, but can be solely about traits of others as well. “Lucy is a bitch” is trait-information and is not always exclusive social knowledge. It is exclusive social knowledge if the receiver did not know Lucy was a bitch before. It is no exclusive social knowledge if the receiver did already know Lucy was a bitch before. If merely traits about a gossipee are shared, and even if these traits are known to the receivers, a sender of RG does not really signal social knowledge. “Lucy is a bitch because she stole her best friend’s boyfriend” is trait-and-behavior information and does signal exclusive social knowledge. Social knowledge is automatically present when traits are combined with behaviors, and this is also the case for changed-traits information. For instance: “Remember pretty Lucy? She is quite an ugly girl now” is trait-information, but signals that a trait of someone has been changed, and this is because he or she did something to change a trait. In such changed-traits cases the sender does signal exclusive social knowledge.
A second benefit that can be gained from sharing RG is that the sender can bask in the glory of his family members and friends’ successes. Increasing the reputation of his or her allies, the sender of RG relatively increases his or her own reputation. If the gossipee is kin related to the sender, he or she even gains an extra benefit. Third and last, senders of RG benefit from attacking foes. This is because lowering the status of disliked non-allies relatively increases the senders’ own reputation. Potential costs involved in this last benefit emerge when the gossipee of slandering RG is kin related to the sender.
When we manipulate the reputations and social identities of others it is important to keep in mind that, because of inclusive fitness, we not only damage the reputation of the person who is targeted in the gossip, but also his or her relatives (Merry, 1984). “A young woman’s sexual deviance, for example, destroys the honor of her whole kin group in many Mediterranean societies.” (Merry, 1984: p. 280). Because for RG the gossipees themselves are at stake (which is different for sharing SLG), it is important for the sender of RG to take into account his or her degree of relatedness with the gossipee of RG. For SLG the senders had to take into account their relatedness to the receivers, here it is the relatedness to the gossipee that is central.
It is important to remark that effects of change in the reputation of the gossipee will only occur for receivers who believe the RG. If they believe the sender, and therefore believe the manipulative content of the RG, receivers will calibrate their attitude towards the gossipee, which in the end changes the reputation of the gossipee. Receivers who do not believe the sender of RG will not recalibrate their opinion about the gossipee, and they have no effect on the reputation of the gossipee.
As a last important remark, I recapitulate that I mentioned in chapter 4 that the manipulative use of RG concerns liked allies (friends) and disliked non-allies (foes), but is not used for neutral non-allies.
5.1.1.2 Costs of sharing RG
For sharing RG I define four different costs. First of all the sender of RG risks a decrease in personal prestige if his or her receiver(s) do(es) not believe him or her. If the receiver disbelieves the sender, the sender gets labeled as a liar, which decreases his social status of having social knowledge. This cost is also involved in the sharing of SLG and any other information. Secondly, sharing RG can be costly if the gossipee is kin related to the sender of RG, as I already mentioned in the previous section. If the sender shares slanderous RG and the gossipee of this reputation-lowering RG is kin related to the sender, his or her own relative reputation goes down as well.
A third cost implied in the sharing of RG concerns potential retaliations of the gossipee.
“This is because it is likely that the reputation of the person being talked about will, in time, have effects on that person. The effect of reputation usually brings his or her behaviour more into line with social expectations. Those taking part have an implicit understanding of the effects of gossip, and the possibility that they too may become the subject of gossip.” (Bromley, 1993: 99)
If the RG increases the status of the gossipee, the sender is not likely to expect retaliations of the gossipee. But is the RG is lowering the reputation of the gossipee, the sender can expect a retaliation of the gossipee. The degree of this retaliation is dependent on the degree wherein the reputation of the gossipee has been lowered and towards how many receivers. If the sender only told one or two persons, the gossipee might not retaliate as strong as when the sender has shared the negative RG with for instance 50 others. Also the degree wherein the RG lowers the reputation of the gossipee is of relevance. Slightly negative RG will elicit fewer retaliation effects than strong negative RG.
A fourth and last cost of sharing RG is, again similar to the sharing of SLG, the risk that someone else runs away with the sender’s knowledge. Other people will use your knowledge to signal intelligence to others as well.
5.1.2 Fewer costs of reliability for Reputation Gossip
Although I have restricted the topic of this dissertation to gossip, which I have defined as information of which the sender has clear truth/false knowledge (see chapter 1), I want to make a remark about the importance of the reliability for RG and SLG.
When comparing SLG and RG, an important difference concerns the reliability of the gossip content. For SLG, unreliable information holds the potential threat that the fitness of receivers is at stake. Sharing information that a certain strategy is fitness-promoting while it actually is not, can endanger the receivers’ fitness. Only when the sender of SLG has truth/false knowledge he or she should share his or her information with others. When the truth/false knowledge is lacking he or she best not shares the SLG. Remark that when the truth/false knowledge is lacking, I don’t talk about gossip but about rumors.
In contrast with SLG, the reliability of the information is not as important for RG. Sharing unreliable information (rumors) about the reputations of gossipees has less important consequences. What is important for RG is whether receivers believe the information or not. If the information is unreliable and many believe the gossip, the reputation of the gossipee changes, regardless of whether the information is actually true or not. Consider “Brad is such a mean guy”. Sharon shares this negative RG with 20 other people who all believe her. In this case the reputation of Brad goes down in the eyes of 20 people. Whether Brad is really mean or not does not matter. What matters is the amount of people who believe Sharon. This is different from for instance “Brad got promoted because he always dares to criticize his boss, and apparently this boss really appreciates this!”. When Sharon shares this with 20 people who all believe her, some might mimic Brad’s strategy. If this SLG is true and Brad’s boss promotes personnel if they dare to criticize him, this will benefit the receivers mimicking Brad. If this SLG is not true, however, receivers mimicking Brad risk loosing their job. In this second case of SLG it is important for Sharon to be sure about the information, because the consequences of her sharing it are important.
Because reliability is less important for RG, I have not incorporated this in the mathematical model I will now present.
5.1.3 Mathematical model for sharing Reputation Gossip
I put forward two mathematical models to outline the optimal strategy to share Reputation Gossip. I present two models, one for sharing good RG that increases the reputation of the gossipee, and a different model for bad RG that decreases the reputation of the gossipee. I put forward two models because RG either increases or decreases the reputation of a gossipee and both do not occur in the same piece of information. Putting the above described costs and benefits into mathematical models where benefits should outscore the costs to the sender, I propose the following two models:
5.1.3.1 Mathematical model for sharing good RG
My mathematical model to describe the optimal strategy to share good Reputation Gossip is the following formula:
(bCM + bNCM).SK + (bCM + bNCM).[PRcm + k(cm)]
>
(dCM + dNCM).SK + (bCM + bNCM).[PRncm - k(ncm)]
Where:
SK= Social Knowledge
Senders of RG show of exclusive Social Knowledge.
SK can vary from 0 to 1.
SK = 0 if the only trait-information is present and the receiver already knows the RG information
SK = 0 if changed-trait or trait-and-behavior information is present and everyone already knows the RG information
SK = 1 if the sender has exclusive RG information
Note that SK at the left side of the ‘>’ (benefits) means bonus points, or benefits to the sender: he or she gets merit for having Social Knowledge in the eyes of the receivers who believe him. The more receivers believe him, the more merit the sender gets (SK gets multiplied with (bCM + bNCM)
SK at the right side of the ‘>’ (costs) means punishment for being seen as a liar, or costs to the sender: he or she gets punishments from all receivers who do not believe the gossip message (SK here gets multiplied with (dCM + dNCM)
CM = coalition member receivers
NCM = non-coalition member receivers
b = number of people who believe you
d = number of people who disbelieve you
PR= degree of positivism of Reputation Gossip
cm= coalition member gossipee
ncm= non coalition member gossipee
k(cm)= degree of kin relatedness to coalition member gossipee
k(ncm) degree of kin relatedness to non-coalition member gossipee
In this model one benefit of sharing good RG is that the sender can gain social status for showing off social knowledge from all receivers believing him or her: (bCM + bNCM).SK. Again, SK can vary from value ‘0’ to value ‘1’. If only-trait information is shared, and the receiver already knew, then SK= 0. If changed-trait or trait-and-behavior RG is shared, and everyone already knows, SK= 0. If the RG information is only known by the sender SK= 1.
The second benefit stems from an increase in reputation (PR) of the gossipee if this gossipee is a coalition member (cm). I labeled “PR” as the “degree of positivism of the RG”. When testing this model (see examples below) by putting in (fictive) numbers, PR can vary from low positive to high positive. To do this with real life data, an easy way to define PR (and NR which I use in the model below) is to present different kinds of RG and ask respondents to rate on a scale varying from “-3” to “+3” how good or bad they consider the trait/behavior content. In paper 7 of this dissertation I presented respondents good and bad RG stories. To have an indication of how good (PR) and how bad (NR) these RG stories were, I asked some control group respondents to rate these traits/behaviors on a negative/positive scale. For instance “saving someone who is drowning” and “being a good host, preparing great meals and entertaining your guests” are both rated positive, but the first is rated more positive than the second (see paper 7 for more details), so the first would get a higher PR score than the second.
Additional benefits are present if the sender is kin related to the coalition member gossipee (cm) of good RG. The higher the degree of relatedness with the coalition member gossipee, the higher the extra benefit (represented by Wright’s r).
Costs of sharing good RG I in this model are increasing the reputation of non-liked non-coalition members: (bCM + bNCM).PRncm. The more people the sender shares the good RG with and who believe him or her, the more the reputation of the gossiped about non-coalition member increases and the more the sender’s own relative reputation decreases. If this non-coalition member is kin related to the sender, some costs are reduced.
A second cost I have modeled here is the social knowledge status loss for the sender in the eyes of all receivers who do not believe the sender: (dCM + dNCM).SK.
5.1.3.2 Mathematical model for sharing bad RG
The mathematical model for sharing bad Reputation Gossip that I suggest looks as follows:
(bCM + bNCM).SK + (bCM + bNCM). [NRncm – k(ncm)]
>
(dCM + dNCM).SK + (bCM + bNCM).RT + (bCM + bNCM).[NRcm + k(cm)]
Where:
SK= Social Knowledge
Senders of RG show of exclusive Social Knowledge.
SK can vary from 0 to 1.
SK = 0 if the only trait-information is present and the receiver already knows the RG information
SK = 0 if changed-trait or trait-and-behavior information is present and everyone already knows the RG information
SK = 1 if the sender has exclusive RG information
Note that SK at the left side of the ‘>’ (benefits) means bonus points, or benefits to the sender: he or she gets merit for having Social Knowledge in the eyes of the receivers who believe him. The more receivers believe him, the more merit the sender gets (SK gets multiplied with (bCM + bNCM)
SK at the right side of the ‘>’ (costs) means punishment for being seen as a liar, or costs to the sender: he or she gets punishments from all receivers who do not believe the gossip message (SK here gets multiplied with (dCM + dNCM)
CM = coalition member receivers
NCM= non-coalition member receivers
b = number of people who believe you
d = number of people who disbelieve you
NR= degree of negativism of Reputation Gossip
cm= coalition member gossipee
ncm= non coalition member gossipee
k(cm)= kin relatedness to coalition member gossipee
k(ncm) kin relatedness to non-coalition member gossipee
RT= Retaliation effect
In this model a first benefit of sharing bad RG is again that the sender can gain social status for showing off social knowledge (if present in RG) from all receivers believing him or her: (bCM + bNCM).SK. The second benefit stems from a decrease in reputation (NR) of disliked non-coalition members. By decreasing the reputation of your foes, with which you do not associate yourself, you can increase your personal relative reputation. I labeled “NR” as a “degree of negativity”. NR varies from low negative to high negative, just like PR does (see above). This benefit has to be corrected with the kin relatedness to the non-coalition member gossipee: k(ncm). The higher the degree of kin relatedness to the non-coalition member gossipee, the higher this cost will be.
A first cost incorporated in this model again concerns a decrease in status in the eyes of all receivers who do not believe the sender: (dCM + dNCM).SK. Secondly, the sender risks retaliation costs (RT) that will depend on the number of people who receive and believe the negative RG. The retaliation threats (RT) will also vary according to the degree of negativity (NR) of the bad RG. The more negative the RG is, the more the reputation of the gossipee will be decreased and the more this gossipee might want to retaliate on the sender.
A last cost occurs when the sender lowers the reputation of a coalition member by sharing bad RG. This rebounds to a personal decrease in relative status. If this coalition member gossipee (cm) is kin related to the sender an additional cost is implied to the sender, depending on the degree of kin relatedness.
5.1.3.3 Optimal strategy to share RG
From these models it follows that the optimal strategy for a sender of RG is to tell the news to as many people as possible of whom a sender thinks they will believe him or her. Each receiver who believes the sender will be impressed by his or her social knowledge. It is more beneficial to the sender when as many people hear it from him or her than when they hear it from someone else. “Hey I’ll tell you something, but don’t spread this around’ (because I will)”.
Senders optimally share RG when the content of the RG elevates coalition members’ status and this leads to an increase of his or her own relative status. An extra benefit can be gained if the coalition member is a kin-related person. Similarly, senders best share RG when the content of the RG lowers non-coalition members’ reputation and this leads to an increase of the senders own relative status. However, there might be a cost related to this when the non-coalition member is kin-related to the sender.
5.1.4 Some examples of the mathematical models that explain optimal sharing strategies for Reputation Gossip
To illustrate the above outlined mathematical models for sharing RG, I will now present some fictive examples of optimal and non-optimal strategies to share good or bad RG. I will first give two examples of sharing good RG, and then two examples of sharing bad RG. For all examples I will use forms of RG where exclusive social knowledge is transmitted.
5.1.4.1 Example 1: Optimal strategy for sharing good RG
Consider RG “My sister is such a sweet girl, she helped Ann with her homework”. A sender X is the only witness of this (SK= 1) and shares this good RG with PR=1 (low positive) about his sister, a coalition member gossipee (cm) with whom the sender is related with r=.5 [k(cm)=.5] with 10 coalition members and 5 non-coalition members. Of these 10 coalition member receivers (CM) 7 believe X1 (bCM=7) and 3 disbelieve X (dCM=3). Of the 5 non-coalition members 4 disbelieve X (dNCM=4) and 1 believes X (bNCM=1).
X gets merit from each receivers who believes him because he shares some exclusive social knowledge (SK= 1), and punishment from each receiver who disbelieves him.
If I put this information in the mathematical formula I have outlined above this gives:
(bCM + bNCM).SK + (bCM + bNCM).[PRcm + k(cm)]
>
(dCM + dNCM).SK + (bCM + bNCM).[PRncm - k(ncm)]
(7 + 1).1 + (7+1).[1 + .5]
>/<?
(3 + 4).1 + (7.1).0
8 + 8 + 4
>/<?
7
20 > 7
Benefits (20) clearly outscore the costs (7).
If X would share an even more positive RG, such as “My sister is such a hero, she saved the life of a little boy who nearly drowned in the lake!” Such a good RG, most probably gets a higher PR value. Hypothetically consider that we would label this good RG to have PR value of “3”: and then the benefits in the above described example rise to 36.
The examples I mention here are pure hypothetical. Still, I believe they can be tested with real life data, or computer programs plausibly varying all the values given to the parameters to detect significant patterns about when it is beneficial to spread which kind of RG. PR has to vary on a scale that can be construed by presenting different kinds of good RG’s to a control group and asking these control respondents to rate the statements on a Likert-scale.
5.1.4.2 Example 2: Non-optimal strategy for sharing good RG
To illustrate what would be a non-optimal strategy to share good RG with others, I take the same example as the one above. Consider X shares “Lucy is such a nice girl; she helped Ann with her homework”. Lucy is a foe of X, and non-related to X. Again this is shared with 10 coalition members (who also dislike Lucy) and 5 non-coalition members (suppose they like Lucy). If now the believe/disbelieve rates remain the same bCM=7, dCM=3; bNCM=1; dNCM=4.
(bCM + bNCM).SK + (bCM + bNCM).[PRcm + k(cm)]
>
(dCM + dNCM).SK + (bCM + bNCM).[PRncm - k(ncm)]
(7 +1).1 + (7+1).0
>/<?
(3 + 4).1 + (7 + 1).[1 – 0]
8
>/<?
7 + 8
8 < 15
Here benefits are lower than the costs. Even though X is nice by sharing good RG, this actually is not an optimal strategy. Increasing the status of foes, even with moderate positive RG (PR=1) relatively decreases your own relative status. The sender’s foe gets a good reputation (in this example the gossipee gets 8 bonus points), he himself only gets 8 bonus points for showing off some social knowledge (I know Lucy and know what she did, and know she is connected to Ann), but also 7 punishment points of those who disbelieve him.
5.1.4.3 Example 3: Optimal strategy for sharing bad RG
Turning to bad RG, consider X shares “I hate Lucy, she is such a bitch, she stole Erica’s boyfriend!” X then lowers Lucy’s reputation. Consider that Lucy is a non-coalition foe of X and is not kin related to X [k(ncm)= 0]. Lucy has never retaliated in bad gossip spread about her in the past (RT=0). Assuming that NR= 1; 7 coalition members believe X (bCM=7); 3 coalition members disbelieve X (dCM=3); 4 non coalition members disbelieve X (dNCM=4) and 1 non-coalition member believes X (bCM=1), the mathematical model for sharing bad RG can be filled in as follows:
(bCM + bNCM).SK + (bCM + bNCM). [NRncm – k(ncm)]
>
(dCM + dNCM).SK + (bCM + bNCM).RT + (bCM + bNCM).[NRcm + k(cm)]
(7 + 1).1 + (7 + 1).[1 + 0]
>/<?
(3 + 4).1 + (7 + 1).0 + (7 + 1).0
8 + 8
>/<?
7
16 > 7
This is an optimal strategy of X. However, if Lucy is known to retaliate on bad gossip about her, by spreading equally bad RG about the sender who slanders her, I can put in a RT=1 in this model. Then the calculation is as follows:
(bCM + bNCM).SK + (bCM + bNCM). [NRncm – k(ncm)]
>
(dCM + dNCM).SK + (bCM + bNCM).RT + (bCM + bNCM).[NRcm + k(cm)]
(7 + 1).1 + (7+1).1
>/<?
(3+4).1 + (7+1).1
16
>/<?
7 + 8
16 > 15
The strategy remains beneficial to X. However, if Lucy is known to retaliate even stronger on those who slander her, by spreading even worse RG about the sender, X might be better of not sharing this moderate negative RG about Lucy. If for example RT=2, then:
(bCM + bNCM).SK + (bCM + bNCM). [NRncm – k(ncm)]
>
(dCM + dNCM).SK + (bCM + bNCM).RT + (bCM + bNCM).[NRcm + k(cm)]
(7 + 1).1 + (7+1).1
>/<?
(3+4).2+ (7+1).1
16 < 23
Costs here outscore benefits.
5.1.4.4 Example 4: Non-optimal strategy for sharing bad RG
Now consider X shares this bad RG with NR=1 about a coalition member: “Mary is such a bitch, she slept with her best friend’s boyfriend”. Additionally consider X is kin related to Mary with r=.5 (Mary is a sister). By lowering the reputation of this person with whom X is associated, he lowers his own relative reputation, here with NR= 1.
Again assume that 7 coalition members believe X (bCM=7); 3 coalition members disbelieve X (dCM=3); 4 non coalition members disbelieve X (dNCM=4) and 1 non-coalition member disbelieves X (dCM=1), the mathematical model for sharing bad RG can be filled in as follows:
(bCM + bNCM).SK + (bCM + bNCM). [NRncm – k(ncm)]
>
(dCM + dNCM).SK + (bCM + bNCM).RT + (bCM + bNCM).[NRcm + k(cm)]
(7+1).1 + (7 + 1).0
>/<
(3+4).1 + (7+1).(1+.5)
8
>/<
7 + 12
8 < 19
X lowers the reputation of a kin related ally, by spreading this bad news, and therefore lowers his own relative status. I have not even put in potential retaliation costs, which could even make this a worse strategy for X. And even when Mary would have been a non kin related friend, costs would still have outscored benefits (8< 15). This illustrates that sharing bad RG about allies is not an optimal strategy. When your friends do bad things, you better do not share this with others, to secure that your own relative status (because you are associated with your friends) does not suffer.
People bask in the glory of the success of their friends and the failures of their enemies. Likewise they suffer from the failures of their friends, and successes of their foes. By sharing RG about the success of friends and failures of enemies, individuals can increase their own relative status. Remaining silent about the failures of friends and successes of foes secures an individual that his or her own relative status does not suffer from the actions of others. With the above examples I have tried to illustrate this. Stronger support stems from the research of McAndrew and Milenkovic (2002), who have shown that individuals indeed share good gossip about friend and bad gossip about foes, and do not share good gossip about foes and bad gossip about friends. In paper 8 of this dissertation, I will investigate if the same is true for sharing Reputation Gossip about celebrities.
5.1.5 Classification trees for sharing Reputation Gossip
As I have argued above for SLG, of course people do not make full cost/benefit analyses before they decide to share gossip. If we would compute a mathematical model for each gossip we want to share, we would loose a lot of time and energy. And gossip seems to spread very spontaneously in real life: “Gossip seems to circulate because people are fundamentally interested in each other and are always ready to tell things and to listen. Anything interesting spread itself abroad, as it were, spontaneously. (MacGill, 1968: 105).
To outline human decision making that resembles more how we solve problems of when to share RG and when not to share RG, I again put forward classification trees. The trees I presented for SLG were no fast and frugal trees, because leaf nodes were not present at each level. The trees introduce here are fast and frugal trees with leaf nodes at each level.
Again these trees line up all necessary criteria people have to take into account when they have to make decisions of when to share RG and when to pay attention to RG. I start with two fast and frugal trees that represent optimal strategies to share RG.
5.1.5.1 Fast and frugal tree for sharing good RG
The first criterion I have put at the root node of my fast and frugal tree for sharing good RG is the question “Will the receiver believe the RG?” If the answer to this question is “No” a fast and frugal best solution is not to share the RG with the receiver. The sender then rules out all potential costs of losing status for showing off false social knowledge in the eyes of disbelievers. Moreover disbelievers do not recalibrate their attitude towards the gossipee of RG, and therefore are a waste of investment.
Assuming that the receiver will believe the sender, the second and last criterion is “Is the gossipee an ally of me?” If “Yes”, then share the good RG (left branch in tree), if “No” then not share the RG (right branch). Doing this the sender rules out potential costs of increasing the reputation of non-allies which rebounds to a relative decrease in his or her own status. In figure V.6 this tree is represented graphically.
Following these two simple criteria costs are ruled out. Interesting to note is that for sharing RG no ally/non-ally restrictions are made towards the audience. Different from sharing SLG, senders of RG do best by sharing their gossip stories with as many people as possible, both allies and non-allies. Yet it could be argued that the latter category of receivers might contain more disbelievers.
Figure V.6. Fast and frugal tree for sharing good Reputation Gossip
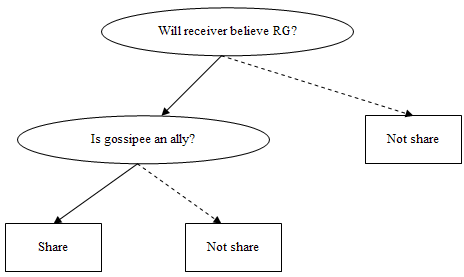
5.1.5.2 Fast and frugal tree for sharing bad RG
For sharing bad RG, I set up a similar fast and frugal decision tree. Again the first criterion is “Will the receiver believe the RG?” If the answer to this question is “No” (right branch in tree) a fast and frugal best solution is not to share the RG with the receiver. This rules out potential costs of loosing social status for having exclusive social knowledge, because you will get labeled as a liar by those disbelievers.
The second criterion is “Is the gossipee a non-ally (foe) to me?” If “Yes”, go to next criterion (left branch that goes to child node in tree), if “No” then decide not to share. Here information is only shared in the gossipee is a foe, which is opposite from sharing good RG.
To this tree I added a third criterion. Different from good RG, bad RG has an extra potential cost to the sender: a retaliation threat of the gossipee. Therefore a third and last criterion can be “Has the gossipee retaliated on bad RG in the past?” If “Yes”, play safe and not share the RG, if “No”, share the bad RG. All criteria are lined up in figure V.7.
Figure V.7. Fast and frugal tree for sharing bad Reputation Gossip
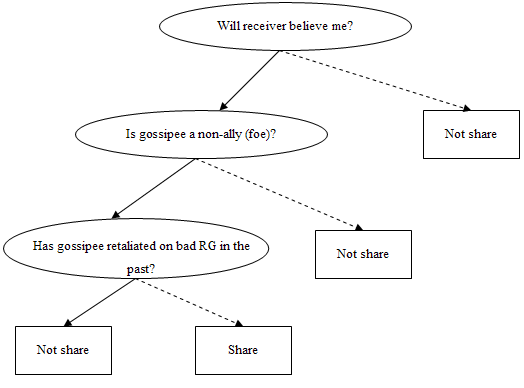
5.2 Acquiring Reputation Gossip
Turning to the receivers’ side of RG, I will now discuss what the costs and benefits for the receivers are and put forward a fast and frugal decision tree to outline the optimal strategy when to pay (extra) attention to RG.
5.2.1 Costs and benefits of acquiring Reputation Gossip
The benefit of acquiring Reputation Gossip is that a receiver can learn about specific other individuals who are part of his or her social network. In our interactions with others it is important that we can correctly ‘mind-read’ others. Because we cannot constantly follow up one everyone at the same time, gossip functions to recalibrate our thoughts and attitudes towards our social network member. Learning who has cheated, who has acted altruistic, who has developed new skills; who lost skills and so on is fitness-relevant for our future interactions with these people. Also learning about new people we have not yet encountered but with whom future encounters can be secured is valuable.
Since for all kinds of gossip, and other forms of communication, the cost of acquiring information is that it might be false information, this is the cost for acquiring Reputation Gossip as well. The reliability of the source is at stake, and receivers must take into account the reliability of RG sources.
5.2.2 Fast and frugal tree for acquiring Reputation Gossip
In the fast and frugal tree I will present for acquiring Reputation Gossip, I have put reliability of the sources as first, and most important criterion. Receivers’ best strategy is to ignore RG that stems from unreliable sources. When they think reliability is low they should not (re)calibrate their attitude towards the gossiped about gossipee. Still, I would like to comment that reliability is of greater importance for SLG than for RG. Receivers of SLG have to decide whether they will mimic gossiped about strategies in the future or not. The personal consequences are greater than the consequences of RG, which concern calibration of attitudes towards others. However, even though reliability might be slightly less important for RG than for SLG, it still remains top priority for receivers of RG.
As a second criterion I have put in past encounters with the gossipee (see figure V.8). Estimating if future encounters with the gossipee are likely is not always easy and accurate. If the receiver has already encountered the gossipee in the past, future encounters are likely. Therefore, if the receiver believes the RG source and has had past encounters with the RG gossipee, a fast and frugal decision is to store the RG information and calibrate his or her attitude towards the gossipee.
If past encounters are not a fact, the receiver best estimates chances of future encounters with the gossipee. If future encounters are not likely, the receiver optimally ignores the RG. If future encounters are likely, the best strategy for the receiver is to store this RG knowledge and to calibrate his or her attitude towards the gossipee. For a graphical overview of all the decisions a receiver of RG best makes, I refer to figure V.8.
Figure V.8. Fast and frugal tree for acquiring Reputation Gossip
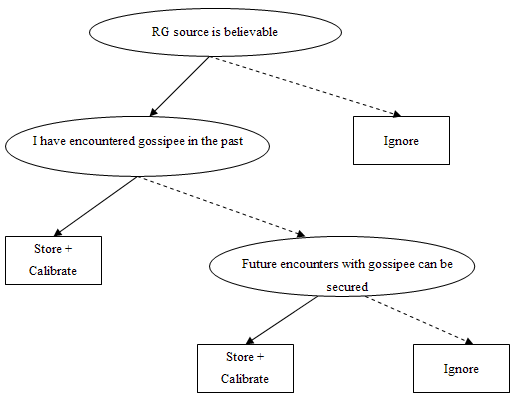
6 Reputation and Strategy Learning Gossip combined
In all models presented in this chapter, I have separated SLG and RG. Both have different functions and are shared and acquired for different reasons. Still, I want to end this chapter by making the remark that in reality most gossip stories (as nouns) are a mixture of both SLG and RG. Therefore most gossip stories have multiple functions. The sharing and acquiring of most gossip stories will therefore follow both the decision processes of SLG and RG. Still, I have introduced different models to clearly outline the decision processes that are optimal for the different kinds of gossip.
| home | list theses | contence | previous | next |